Câu hỏi:
11/07/2024 52,153
Trả lời:
![]()
Giải vày Vietjack
Do tam giác ABC cân nặng bên trên A nên AB = AC.
Do M là trung điểm của BC nên MB = MC.
Xét nhị tam giác ABM và ACM có:
AB = AC (chứng minh trên).
AM cộng đồng.
MB = MC (chứng minh trên).
Do cơ (c – c – c).
Khi cơ (2 góc tương ứng).
Mà (2 góc kề bù) nên
Do đó
Do nên (2 góc tương ứng).
Do cơ AM là tia phân giác của
Vậy AM vuông góc với BC và AM là tia phân giác của góc BAC.
Nhà sách VIETJACK:
🔥 Đề thi đua HOT:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC cân nặng bên trên A và những điểm E, F theo thứ tự phía trên những cạnh AC, AB sao mang lại BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
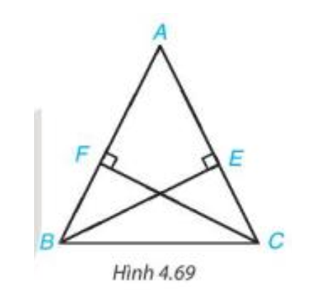
Cho tam giác ABC cân nặng bên trên A và những điểm E, F theo thứ tự phía trên những cạnh AC, AB sao mang lại BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
Câu 2:
Cho tam giác ABC cân nặng bên trên A sở hữu lối cao AD. Chứng minh rằng đường thẳng liền mạch AD là lối trung trực của đoạn trực tiếp BC.
Câu 3:
Tam giác vuông sở hữu nhị cạnh đều bằng nhau được gọi là tam giác vuông cân nặng.
Hãy phân tích và lý giải những xác định sau:
a) Tam giác vuông cân nặng thì cân nặng bên trên đỉnh góc vuông;
b) Tam giác vuông cân nặng sở hữu nhị góc nhọn vày 45o;
c) Tam giác vuông sở hữu một góc nhọn vày 45o là tam giác vuông cân nặng.
Tam giác vuông sở hữu nhị cạnh đều bằng nhau được gọi là tam giác vuông cân nặng.
Hãy phân tích và lý giải những xác định sau:
a) Tam giác vuông cân nặng thì cân nặng bên trên đỉnh góc vuông;
b) Tam giác vuông cân nặng sở hữu nhị góc nhọn vày 45o;
c) Tam giác vuông sở hữu một góc nhọn vày 45o là tam giác vuông cân nặng.
Câu 4:
Tính số đo những góc và những cạnh chưa chắc chắn của tam giác DEF nhập Hình 4.62.
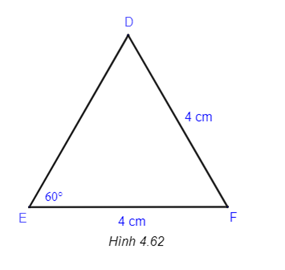
Tính số đo những góc và những cạnh chưa chắc chắn của tam giác DEF nhập Hình 4.62.

Câu 5:
Cho M là 1 điểm phía trên lối trung trực của đoạn trực tiếp AB. hiểu AM = 3 centimet và (H.4.67). Tính BM và số đo góc MBA.
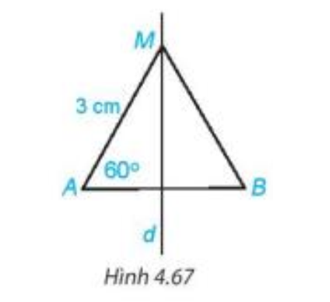
Cho M là 1 điểm phía trên lối trung trực của đoạn trực tiếp AB. hiểu AM = 3 centimet và (H.4.67). Tính BM và số đo góc MBA.
Câu 6:
Cho tam giác ABC và M là trung điểm của đoạn trực tiếp BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân nặng bên trên A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân nặng bên trên A.
Cho tam giác ABC và M là trung điểm của đoạn trực tiếp BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân nặng bên trên A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân nặng bên trên A.
CHỌN BỘ SÁCH BẠN MUỐN XEM
Hãy lựa chọn đúng đắn nhé!
