Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng: a) HA . HD = HB . HE = HC . HF; b) ∆AFC ᔕ ∆AEB và AF . AB = AE . AC; (Miễn phí)

Lời giải

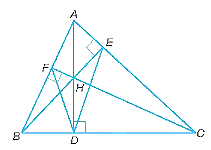
a)

Vì AD, BE, CF là những đàng cao của tam giác ABC nên AD vuông góc với BC, BE vuông góc với AC, CF vuông góc với AB.

Tam giác AHE vuông ở H và tam giác BHD vuông ở D có:

\(\widehat {AHE} = \widehat {BHD}\) (hai góc đối đỉnh)

Do tê liệt, ∆AHE ᔕ ∆BHD (góc nhọn).

Suy đi ra \(\frac{{AH}}{{BH}} = \frac{{HE}}{{HD}}\) nên HA . HD = HB . HE (1).

Tam giác HBF vuông ở F và tam giác HCE vuông ở E có:

\(\widehat {BHF} = \widehat {EHC}\) (hai góc đối đỉnh)

Do tê liệt, ∆HBF ᔕ ∆HCE (góc nhọn).

Suy đi ra \(\frac{{HB}}{{HC}} = \frac{{HF}}{{HE}}\) nên HB . HE = HC . HF (2).

Từ (1) và (2) tớ có: HA . HD = HB . HE = HC . HF.

b)

Tam giác AFC vuông ở F và tam giác AEB vuông ở E có:

\(\widehat {BAC}\) cộng đồng.

Do tê liệt, ∆AFC ᔕ ∆AEB (góc nhọn)

Suy đi ra \(\frac{{AF}}{{AE}} = \frac{{AC}}{{AB}}\) nên AF . AB = AE . AC.

c)

Vì HA . HD = HB . HE nên \(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\)

Tam giác HAB và tam giác HED có:

\(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\) (cmt)

\(\widehat {AHB} = \widehat {EHD}\) (hai góc đối đỉnh)

Do tê liệt, ∆AHB ᔕ ∆EHD (c.g.c).

Suy đi ra \(\widehat {HAB} = \widehat {HED}\).

Mà \(\widehat {HAB} + \widehat {FBD} = \widehat {HED} + \widehat {DEC}\) (= \(90^\circ \)).

Do tê liệt, \(\widehat {FBD} = \widehat {DEC}\).

Chứng minh tương tự động tớ có: \(\widehat {BFD} = \widehat {ECD}\).

Tam giác BDF và tam giác EDC có:

\(\widehat {FBD} = \widehat {DEC}\) (cmt)

\(\widehat {BFD} = \widehat {ECD}\) (cmt)

Do tê liệt, ∆BDF ᔕ ∆EDC (g.g).

Suy ra: \(\widehat {BDF} = \widehat {EDC}\).

Mà \[\widehat {BDF} + \widehat {FDH} = \widehat {EDC} + \widehat {HDE}\left( { = 90^\circ } \right)\].

Do tê liệt, \(\widehat {FDH} = \widehat {HDE}\) hoặc \(\widehat {FDA} = \widehat {ADE}\).

Vậy DA là tia phân giác của góc EDF.

Câu 1: