Cho hàm số y = f(x) có đồ thị như hình dưới. Hàm số trên nghịch biến trên khoảng A. (– ∞; 2); B. (2; + ∞); C. (0; 2); D. (– ∞; 0). (Miễn phí)

C. (0; 2);

Đáp án chủ yếu xác

Viết phương trình tổng quát tháo của đường thẳng liền mạch

a) trải qua M(– 1; – 4) và tuy vậy song với đường thẳng liền mạch 3x + 5y – 2 = 0;

b) trải qua N(1; 1) và vuông góc với đường thẳng liền mạch 2x + 3y + 7 = 0.

Phương trình \[\sqrt { - {x^2} + 4x} = 2x - 2\] đem số nghiệm là

A. 0;

B. 1;

C. 2;

D. 3.

Trong mặt mũi phẳng lì tọa chừng, mang lại lối tròn xoe (C): x² + y² – 2x – 4y – 4 = 0 và điểm A(1; 5). Tiếp tuyến của lối tròn xoe (C) bên trên điểm A đem phương trình là

A. hắn – 5 = 0;

B. hắn + 5 = 0;

C. x + hắn – 5 = 0;

D. x – hắn – 5 = 0.

Trong mặt mũi phẳng lì tọa chừng Oxy, mang lại đường thẳng liền mạch d: – x + 2y + 7 = 0. Vectơ pháp tuyến của đường thẳng liền mạch d là

A. \(\overrightarrow n = \left( {1;\,\, - 2} \right)\);

B. \(\overrightarrow n = \left( { - 1;\,\,2} \right)\);

C. \(\overrightarrow n = \left( {2;\,\, - 1} \right)\);

D. \(\overrightarrow n = \left( {2;\,\,1} \right)\).

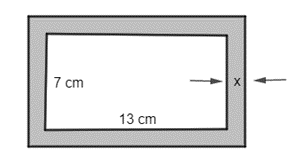
Hà dự tính thực hiện một khuông hình họa hình chữ nhật sao mang lại phần vô của khuông là hình chữ nhật đem độ dài rộng 7 centimet × 13 centimet, phạm vi viền xung xung quanh là x centimet (như hình vẽ). Diện tích của viền khuông hình họa ko vượt lên trên vượt 44 cm². Hỏi phạm vi viền khuông hình họa lớn số 1 là từng nào xen-ti-mét?

Phương trình lối tròn xoe 2 lần bán kính AB với A(1; 3) và B(5; – 1) là

A. (x + 3)² + (y – 1)² = 8;

B. (x + 3)² + (y + 1)² = 8;

C. (x – 3)² + (y + 1)² = 8;

D. (x – 3)² + (y – 1)² = 8.