Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (Miễn phí)

Hướng dẫn giải

Đáp án đích là: B

Gọi x là số xe pháo loại A được mướn, hắn là số xe pháo loại B được mướn. (x ≥ 0, hắn ≥ 0)

Do loại xe pháo A sở hữu 10 cái, loại xe pháo B sở hữu 9 cái nên x ≤ 10, hắn ≤ 9.

Do xe pháo A chỉ chở tối nhiều đôi mươi người và 0,6T sản phẩm, xe pháo B chở tối nhiều 10 người và 1.5 tấn sản phẩm nhưng mà cần thiết mượn xe nhằm chở bên trên 140 người và bên trên 9T sản phẩm nên:

$\{\begin{cases} 20 x + 10 y \geq 140 \\ 0, 6 x + 1, 5 y \geq 9 \end{cases}$

Khi bại tao sở hữu hệ bất phương trình của x và hắn như sau:

$\{\begin{cases} x \geq 0 \\ y \geq 0 \\ x \leq 10 \\ y \leq 9 \\ 20 x + 10 y \geq 140 \\ 0, 6 x + 1, 5 y \geq 9 \end{cases}$ ⇔ $\{\begin{cases} x \geq 0 \\ y \geq 0 \\ x \leq 10 \\ y \leq 9 \\ 2 x + y \geq 14 \\ 2 x + 5 y \geq 30 \end{cases}$

Biểu thao diễn miền nghiệm của hệ bất phương trình bên trên hệ trục tọa phỏng Oxy:

- Biểu thao diễn miền nghiệm D₁ của bất phương trình x ≥ 0.

+ Đường trực tiếp x = 0 là trục Oy.

Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt mũi phẳng phiu bờ Oy (kể cả bờ Oy) nằm cạnh cần trục Oy.

* Tương tự động tao màn trình diễn những miền nghiệm:

- Miền nghiệm D₂ của bất phương trình hắn ≥ 0: là nửa mặt mũi phẳng phiu bờ Ox (kể cả bờ Ox) nẳm bên trên trục Ox.

- Miền nghiệm D₃ của bất phương trình x ≤ 10: là nửa mặt mũi phẳng phiu bờ d₁ (kể cả bờ d₁: x = 10) chứa chấp điểm O.

- Miền nghiệm D₄ của bất phương trình hắn ≤ 9: là nửa mặt mũi phẳng phiu bờ d₂ (kể cả bờ d₂: hắn = 9) chứa chấp điểm O.

- Miền nghiệm D₅ của bất phương trình 2x + hắn ≥ 14:

+ Vẽ đường thẳng liền mạch d₃: 2x + hắn = 14.

+ Xét điểm O(0; 0): thay cho x = 0, hắn = 0 nhập bất phương trình tao sở hữu 2. 0 + 0 = 0 ≥ 14 là mệnh đề sai nên điểm O(0; 0) ko thỏa mãn nhu cầu bất phương trình 2x + hắn ≥ 14.

Miền nghiệm D₅ của bất phương trình 2x + hắn ≥ 14 là nửa mặt mũi phẳng phiu bờ d₃ (kể cả bờ d₃) ko chứa chấp điểm O.

- Tương tự động miền nghiệm D₆ của bất phương trình 2x + 5y ≥ 30 là nửa mặt mũi phẳng phiu bờ d₄ (kể cả bờ d₄: 2x + 5y = 30) ko chứa chấp điểm O.

Ta sở hữu trang bị thị:

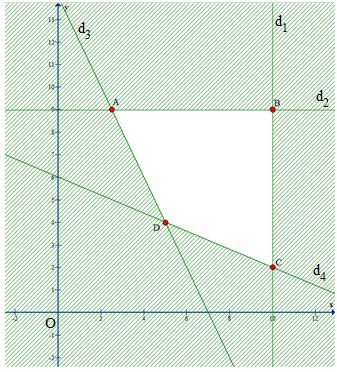
Một doanh nghiệp Trách Nhiệm Hữu Hạn nhập một mùa lăng xê và buôn bán ưu đãi sản phẩm & hàng hóa (ảnh 1)

Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD:

A(2,5; 9), B(10; 9), C(10; 2), D(5; 4)

Một con xe loại A cho tới mướn với giá chỉ 4 triệu, loại B giá chỉ 3 triệu nên tổng số chi phí mướn là:

F (x; y) = 4x + 3y.

Để ngân sách vận fake là thấp nhất thì F (x; y) là nhỏ nhất.

Tại A(2,5; 9): F = 4. 2,5 + 3. 9 = 37;

Tại B(10; 9): F = 4. 10 + 3. 9 = 67;

Tại C(10; 2): F = 4. 10 + 3. 2 = 46;

Tại D(5; 4): F = 4. 5 + 3. 4 = 32;

Vậy F (x; y) đạt độ quý hiếm nhỏ nhất là 32 Khi x = 5 và hắn = 4.

Vậy cần thiết mướn 5 xe pháo loại A và 4 xe pháo loại B nhằm số chi phí mướn nhỏ nhất.

Câu 5:

Một ngôi nhà khoa học tập nghiên cứu và phân tích về hiệu quả kết hợp của Vi-Ta-Min A và Vi-Ta-Min B so với khung hình quả đât. Kết ngược như sau:

- Một người hoàn toàn có thể tiếp cảm nhận được thường ngày không thực sự 600 đơn vị chức năng Vi-Ta-Min A và không thực sự 500 đơn vị chức năng Vi-Ta-Min B.

- Một người thường ngày cần thiết kể từ 400 cho tới 1 000 đơn vị chức năng Vi-Ta-Min cả A và B.

Do hiệu quả kết hợp của nhị loại Vi-Ta-Min, thường ngày, số đơn vị chức năng Vi-Ta-Min B quá nhiều rộng lớn $\frac{1}{2}$ số đơn vị chức năng Vi-Ta-Min A tuy nhiên ko nhiều hơn thế nữa tía phiên số đơn vị chức năng Vi-Ta-Min A.

Biết giá chỉ một đơn vị chức năng Vi-Ta-Min A là 9 đồng và giá chỉ một đơn vị chức năng Vi-Ta-Min B là 7,5 đồng. Phương án sử dụng nhị loại Vi-Ta-Min A, B thoả mãn những ĐK bên trên để sở hữu số chi phí cần trả là tối thiểu là:

A. 500 đơn vị chức năng Vi-Ta-Min A và 500 đơn vị chức năng Vi-Ta-Min B;

B. 600 đơn vị chức năng Vi-Ta-Min A và 400 đơn vị chức năng Vi-Ta-Min B;

C. 600 đơn vị chức năng Vi-Ta-Min A và 300 đơn vị chức năng Vi-Ta-Min B;

D. 100 đơn vị chức năng Vi-Ta-Min A và 300 đơn vị chức năng Vi-Ta-Min B.